More Zen Gamma

It may not be common knowledge, but there have been several noteworthy Indian mathematicians. A few of them were quite peculiar, since they had little or no formal training in their field, like Kaprekar and Ramanujan.

Well, one thing is for sure: formal training kills creativity. And that is exactly what I like about these guys: their ideas were so original and fresh. Arguably, the most fascinating of these two must be Ramanujan - its no wonder they're making a movie about his life. Unfortunately, the man died at a very early age. While still in Madras, Ramanujan recorded the bulk of his mathematical discoveries of the last year of his life in four notebooks of loose leaf paper. And then it was lost and went into the historybooks as "Ramanujan's Lost Notebook".

Its whereabouts were unknown until it was rediscovered by George Andrews in 1976, in a box of effects of G. N. Watson stored at the Wren Library at Trinity College, Cambridge. The discovery of this "Lost Notebook" caused roughly as much stir in the mathematical world as the discovery of Beethoven’s tenth symphony would cause in the musical world.

This notebook contained a formula, describing the limits of the Gamma function. I won't try to replicate it here (it's a Wiki and that one doesn't do mathematical formula's particularly well), but it consists of a rather complex equation which contains a constant. Ramanujan stated that its value was between 1/30 and 1/100.

In 1997 G.D. Anderson, M.K. Vamanamurthy and M. Vuorinen described this function in "Conformal Invariants, Inequalities and Quasiconformal Maps" and in 2008 Ekatherina A. Karatsuba refined it further in "The Ramanujan asymptotic formula for the Euler Gamma function". This rather peculiar function looks like this:

However, calculating it requires.. the Gamma function. It's like chasing your own tail. This won't do. Karatsuba published an article on another way to calculate it, however, the series presented weren't going to be a walk in the park as well. So that's it. Or was it?

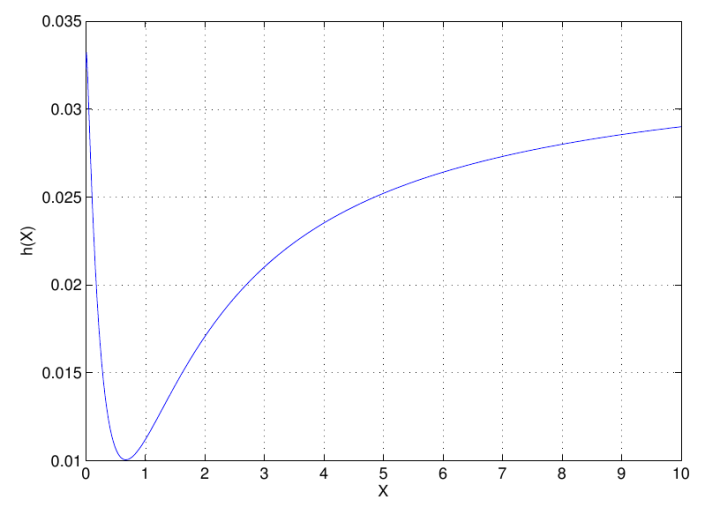
There is another technique called "curve fitting" which basically means you're trying to find another function which fits the curve quite well. But first I tried out how "bad" the 1/30 value really was. Of course it was bad, but with an identity called "Gamma shift" I was able to get acceptable results when shifting it back from "6" to "0".

But how do you get an "alternate function". Well, you can do that even online. Just enter a number of values and find a good one by "trail and error". I decided to split the function up in a domain from "1 to 10" and one from "10 - infinity". Why "1"? Well, as you can see before "1" it starts to behave rather erratically. That's why!

Note that you don't have to do all this straight away in code. We've had spreadsheets for a long time now and you can work out the algorithms needed much more comfortably there. E.g. I worked out the exact values of the function in a spreadsheet - which does feature a gamma function.

I settled for two symmetrical sigmoids and then plotted the whole thing:

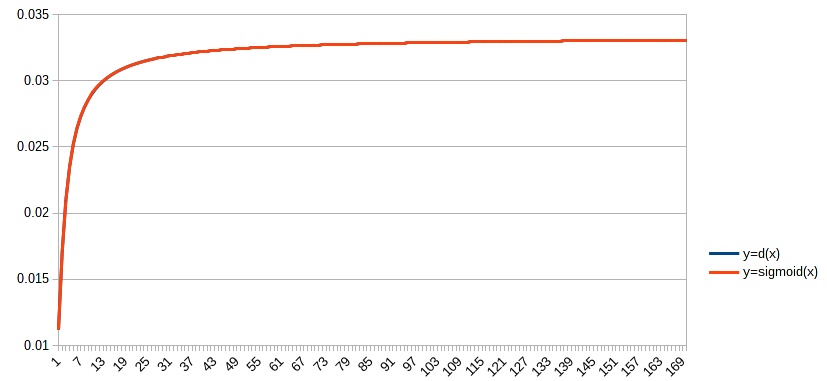
Blue? I don't see any "blue" line. Right. But that doesn't say anything. Rule of the thumb is that if you can see any differences in a graph you're already way off! In reality, the worst (relative) error stayed far below 1e-2 - which is normally not acceptable at all, but note we got "acceptable" results from a 1/30 value (which has a relative error of 3e0), so that's not too bad at all.

So when we put it all together, we only had to shift it back by 2, because Ramanujan's formula doesn't apply to Gamma(X), but to Gamma(X+1). The results were not half bad, a relative error far better than 1e-6, which is between 2 and 100 (close to 0) times better than the standard Zen Gamma function.

So, why keep that last one in? Simple. Because it is 2.5 times faster. So if speed is an issue or accuracy doesn't matter too much, you take the first one - but if it is, you take the second one. So, you got a choice.