Home

Программа работает в среде MS DOS (используйте DosBox с русификатором russian.txt).
Если работает очень медленно или зависает, откройте параметры (F4) и измените Delay на 1. Также, можете дополнительно изменять количество циклов DosBox (Ctrl+F11 / Ctrl+F12).

Данная программа была создана для демонстрации и изучения закономерностей
развития культур клеток, осуществляемой при помощи набора
систем уравнений, являющихся ядром программы. Каждая экосистема
передает программе номер нужной ей cистемы уравнений и параметры
этих уравнений. Таким образом, на основании одной системы уравнений
может быть создано большое количество разнообразных экосистем,
демонстрирующих основные особенности данного типа взаимодействий.

Cодержание справки:
1. Управление программой
2. Структура файлов экосистем
3. Уравнения и модели
4. Замечание об ошибках
5. Источники

1. Управление программой:

   В режиме выбора и редактирования экосистемы:
   F1 - Вызов этой справки
   F4 - Редактирование параметров выбранной экосистемы или смена
   описания папки
   F5 - копирование выбранной экосистемы
   F6 - перемещение выбранной экосистемы
   F7 - создание новой папки
   Ins - создание новой экосистемы
   Del - удаление папки/экосистемы
   BkSp - возврат в предыдущую папку
   Enter - переход в режим моделирования и создание графика числен-
   ностей и концентраций для выбранной экосистемы

   В режиме моделирования экосистемы:
   Esc - Возврат в режим выбора и редактирования
   Enter - Продолжение моделирования с начала экрана
   P - Приостановка моделирования
   Tab - Включение / выключение вывода параметров моделируемой
   экосистемы.
   При нажатии любой клавиши кроме Enter и P моделирование начина-
   ется с начала (с начальных параметров)

2. Программа содержит несколько уравнений моделирования популяций. В файлах
   экосистем номер экосистемы является самым первым параметром (Tip).
   В поставляемых экосистемах после заголовка следуют уравнения дан-
   ного Tip'a. Если вы создаете свой файл, то нужно следовать следу-
   ющим правилам:
   1. Последовательность параметров должна быть всегда определен-
   ной: Tip, отметка о выводимых численностях и концентрациях
   (Show=xxox), состоящая из x-выводить и o-не выводить,
   время (T), переключатель общего/частного максимума по Y
   (ОбщаяY), максимальная отображаемая численность
   (MaxY), начальные количества каждой популяции (No1,
   No2,..), специальные параметры экосистемы. К специальным па-
   раметрам (также в определенной последовательности) относят-
   ся коэффициенты, подставляемые в уравнения динамик популя-
   ций. Переключатель общего/частного максимума сообщает прог-
   рамме, следует ли ей читать из файла MaxY для каждого N
   перед каждым No (кроме No1 - в этом случае MaxY1=MaxY) или
   MaxY является общим масштабным коэффециентом для всех N.
   (Примеры: см. поставляемые экостистемы).
   2. Название перед каждым параметром необязательно, но перед каж-
   дым должен стоять знак равенства, иначе строка рассматрива-
   ется как комментарий.
   3. Комментарии (в том числе пустые строки) можно вводить с любом
   месте файла, начиная с новой строки. Если вы хотите ввести
   комментарий, содержащий знак равенства (уравнение), то нач-
   ните строку со знака ">".

3. Каждому Tip'у соответствует определенный набор уравнений динамики числен-
   ностей штаммов и концентраций веществ экосистемы, количество попу-
   ляций и параметров:
   1. Элементарная модель лимитирования по субстрату без учета ги-
   бели клеток.
   - Ys - экономический коэффициент (определяет, сколь-
   ко субстрата поглощает одна клетка за единицу времени)
   - Mm - предельная максимальная удельная скорость роста.
   - Ks - параметр, характеризующий сродство субстрата к клет-
   кам культуры
   Популяции: 1 (3)
   Уравнения: dS=-N/Ys (субстрат)
   m=MmS/(Ks+S) (скорость роста)
   dN=Nm (число клеток)
   Параметры: Ys, Mm, Ks
   Пример: 1\SUBSTRAT\simple
   2. Логистическая модель лимитирования по субстрату с учетом
   гибели клеток. На основе модели N 1.
   - M1 - "ресурсный" коэффициент. Ограничивает максимальное
   число клеток: Nm=M1/Mm
   Популяции: 1 (3)
   Уравнения: dS=-N/Ys (субстрат)
   m=MmS/(Ks+S) (скорость роста)
   dN=Nm-NNM1 (число клеток)
   Параметры: Ys, Mm, Ks, M1
   Пример: 1\SUBSTRAT\logist
   3. Логистическая модель лимитирования по субстрату с учетом
   ингибирования избытком субстрата. При начальных больших
   количествах субстрата штамм вымирает, при средних коли-
   чествах рост культуры в начале немного ингибируется,
   но, постепенно снижая концентрацию субстрата, бактерии
   постепенно уменьшают силу ингибирования. На основе модели N 2
   - Ki - константа ингибирования избытком субстрата
   Популяции: 1 (3)
   Уравнения: dS=-N/Ys (субстрат)
   m=MmS/(Ks+S(1+S/Ki)) (скорость роста)
   dN=Nm-NNM1 (число клеток)
   Параметры: Ys, Mm, Ks, Ki, M1
   Пример: 1\SUBSTRAT\sii
   4. Логистическая модель ингибирования субстратом при линейном
   контролируемом повышении его концентрации. Фактически
   эта "модель" выводит на экран зависимость скорости роста
   клеток от концентрации субстрата в среде. На основе модели N 3
   - Sk - скорость роста субстрата
   Популяции: 1 (3)
   Уравнения: dS=Sk (субстрат)
   m=MmS/(Ks+S(1+S/Ki)) (скорость роста)
   dN=Nm-NNM1 (число клеток)
   Параметры: Sk, Mm, Ks, Ki, M1
   Пример: 1\SUBSTRAT\siim
   5. Логистическая модель ингибирования стабильным продуктом жиз-
   недеятельности клеток. На основе модели N 2
   - Ki - константа ингибирования продуктом
   - Yp - количество продукта на единицу биомассы
   Популяции: 1 (4)
   Уравнения: dS=-N/Ys (субстрат)
   m=MmS/(Ks(1+P/Ki)+S) (скорость роста)
   dN=Nm-NNM1 (число клеток)
   dP=N/Yp (продукт)
   Параметры: Ys, Mm, Ks, Ki, M1, Yp
   Пример: 1\INGIB\pi
   6. Логистическая модель ингибирования роста клеток продуктом
   их жизнедеятельности, разрушающимся по реакции 1 порядка.
   На основе модели N 5
   - Dp - константа скорости реакции разрушения продукта
   Популяции: 1 (4)
   Уравнения: dS=-N/Ys (субстрат)
   m=MmS/(Ks(1+P/Ki)+S) (скорость роста)
   dN=Nm-NNM1 (число клеток)
   dP=N/Yp-DpP (продукт)
   Параметры: Ys, Mm, Ks, Ki, M1, Yp, Dp
   Пример: 1\INGIB\pid
   7. Логистическая модель лимитирования роста клеток по линейно
   возобновляющемуся субстрату. Субстрат буквально добавляется
   в систему с постоянной скоростью. На основе модели N 2
   - Sd - скорость добавления субстрата
   Популяции: 1 (3)
   Уравнения: dS=-N/Ys+Sd (субстрат)
   m=MmS/(Ks+S) (скорость роста)
   dN=Nm-NNM1 (число клеток)
   Параметры: Ys, Mm, Ks, M1, Sd
   Пример: 1\SUBSTRAT\sr
   8. Модель одного из механизмов индукции. Активное размножение
   клеток не начинается до тех пор, пока концентрация ингиби-
   тора роста не станет достаточно низкой. (логистическая)
   На основе модели N 6
   Популяции: 1 (4)
   Уравнения: dS=-N/Ys (субстрат)
   m=MmS/(Ks(1+З/Ki)+S) (скорость роста)
   dN=Nm-NNM1 (число клеток)
   dP=DpP (ингибитор)
   Параметры: Ys, Mm, Ks, Ki, M1, Dp
   Пример: 1\INGIB\psd
   9. Логистическая модель развития и гибели штамма в результате
   исчерпания субстрата и постепенной инактивации способных к
   делению клеток. На основе модели N 2
   - L - константа скорости инактивации клеток
   Популяции: 1 (4)
   Уравнения: dS=-N/Ys (субстрат)
   m=MmS/(Ks(1+S/Ki)+S) (скорость роста)
   dI=AL-IIM1 (неактивные клетки)
   dA=Am-AAM1 (активные клетки)
   N=I+A (число клеток)
   Параметры: Ys, Mm, Ks, L, M1
   Пример: 1\STOP\ia
   10. Логистическая модель развития и гибели штамма в результате
   инактивации клеток по "запрограммированному отказу". В мо-
   дели предполагается, что скорость размножения клеток прямо
   пропорциональна числу рецепторов к фактору роста на клетках:
   R=A[Exp(-Lt)-Exp(-at)]. На основе модели N 2
   - L - константа скорости потери рецепторов, инактивации
   - a - константа скорости роста количества рецепторов
   - A - коэффициент пропорциональности
   Популяции: 1 (4)
   Уравнения: dz1=-z1L (дополнительные
   dz2=-z2a функции)
   m=A(z1-z2) (скорость роста)
   dN=Nm-NNM1 (активные клетки)
   Параметры: L, a, A, M1
   Пример: 1\STOP\zo
   11. Модель культивирования клеток в режиме хемостата. Неослож-
   ненный рост. Коэффициент D показывает скорость вымывания ве-
   щества и культуры из ферментера, то есть скорость разбавле-
   ния раствора с культурой раствором с субстратом. На основе
   модели N 2
   - D - скорость разбавления
   - Se - концентрация субстрата во входящем растворе
   Популяции: 1 (4)
   Уравнения: m=MmS/(Ks+S) (скорость роста)
   dN=Nm-ND (число клеток)
   dS=D(S-Se)-mN/Ys (субстрат)
   dP=mN/Yp-PD (продукт)
   Параметры: Ys, Mm, Ks, D, Se, Yp
   Пример: 1\STAT\simple
   12. Модель культивирования клеток в режиме хемостата. Рост
   клеток ингибируется продуктом их жизнедеятельности. На
   основе модели N 11, 5. Необходимо помнить, что все компонен-
   ты системы постепенно вымываются из нее, в том числе и продукт
   жизнедеятельности, что и обеспечивает возможность размножения.
   Популяции: 1 (4)
   Уравнения: m=MmS/(Ks(1+P/Ki)+S) (скорость роста)
   dN=Nm-ND (число клеток)
   dS=D(S-Se)-mN/Ys (субстрат)
   dP=mN/Yp-PD (продукт)
   Параметры: Ys, Mm, Ks, D, So, Yp, Ki
   Пример: 1\STAT\pic
   13. Модель лимитирования по субстрату с учетом лизиса клеток
   1 порядка. На основе модели N 1
   - M1 - константа скорости лизиса
   Популяции: 1 (3)
   Уравнения: dS=-N/Ys (субстрат)
   m=MmS/(Ks+S) (скорость роста)
   dN=Nm-NM1 (число клеток)
   Параметры: Ys, Mm, Ks, M1
   Пример: 1\SUBSTRAT\lisis
   14. Логистическая модель динамики численностей двух клеточных
   популяцей, концентраций их субстратов и продуктов. Популя-
   ции взаимодействуют по принципу симбиотрофной ассоциации,
   т.е. продукт жизнедеятельности клеток одного вида является
   субстратом для клеток другого вида. На основе модели N 2.
   Популяции: 2 (7)
   Уравнения: dS1=-N1/Ys1 (субстрат-1)
   m1=Mm1S1/(Ks1+S1) (скорость-1)
   dN1=N1m1-N1N1M1 (клетки-1)
   dS2=-N2/Ys2+N1/Yp1 (продукт-1/
   субстрат-2)
   m2=Mm2S2/(Ks2+S2) (скорость-2)
   dN6=m2N2-N2N2M2 (клетки-2)
   dP2=N2/Yp2 (продукт-2)
   Параметры: Ys1, Mm1, Ks1, M1, Yp1,
   Ys2, Mm2, Ks2, M2, Yp2
   Пример: 2*
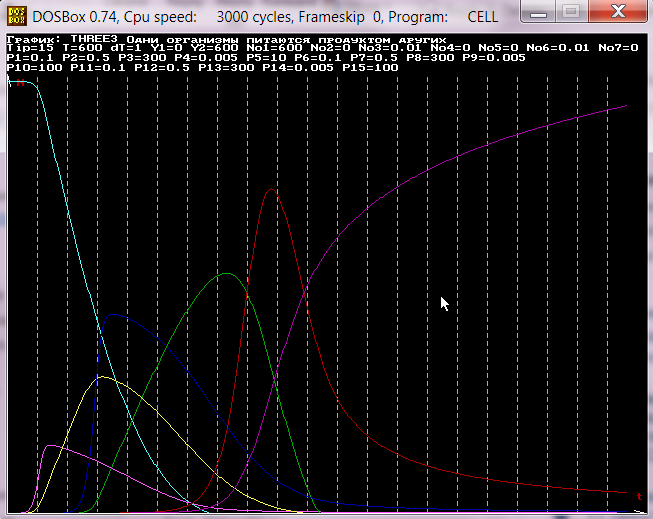
   15. Логистическая модель динамики численностей трех клеточных
   популяцей, концентраций их субстратов и продуктов. Популя-
   ции взаимодействуют по принципу симбиотрофной ассоциации,
   т.е. продукт жизнедеятельности клеток одного вида является
   субстратом для клеток другого вида, а продукт жизнедеятель-
   ности последнего является субстратом для третьего вида.
   На основе модели N 14.
   Популяции: 3 (10)
   Уравнения: dS1=-N1/Ys1 (субстрат-1)
   m1=Mm1S1/(Ks1+S1) (скорость-1)
   dN1=N1m1-N1N1M1 (клетки-1)
   dS2=-N2/Ys2+N1/Yp1 (продукт-1/
   субстрат-2)
   m2=Mm2S2/(Ks2+S2) (скорость-2)
   dN6=m2N2-N2N2M2 (клетки-2)
   S3=-N3/Ys3+N2/Yp2 (продукт-2/
   субстрат-3)
   m3=Mm3S3/(Ks3+S3) (скорость-3)
   dN3=m3N3-N3N3*M3 (клетки-3)
   dP3=N3/Yp3 (продукт-3)
   Параметры: Ys1, Mm1, Ks1, M1, Yp1,
   Ys2, Mm2, Ks2, M2, Yp2,
   Ys3, Mm3, Ks3, M3, Yp3
   Пример: 3*

4. В программе использована специальная многоуровневая система контроля
   ошибок. Поэтому практически ничто не может самопроизвольно завер-
   шить программу без желания пользователя. Если в модель были введе-
   ны неестественные коэффициенты, то результат может выйти за пределы
   (0.5e4932). В этом случае программа выдаст звуковой сигнал и оста-
   новит моделирование, поскольку никаких разумных результатов все равно
   уже нельзя будет получить, исходя из данных параметров. После нажа-
   тия клавиши программа вернется в меню и выдаст сообщение об ошибке,
   предлагая пользователю продолжить работу. Отказываться от продолже-
   ния работы имеет смысл только в том случае, если программа цикличес-
   ки выдает данную ошибку уже несколько раз и не продолжает работу. Та-
   кое в принципе возможно только в случае грубых физических повреждений
   компьютера или изменений программы в результате занесения вируса или
   попыток изменения кода. Если программа обнаружит заражение вирусом,
   она попытается излечить себя с разрешения пользователя, если это ока-
   жется возможным.

5. При составлении программы и подготовке систем были использованы следующие
   источники:
   1. С.Д.Варфоломеев, К.Г.Гуревич. "Биокинетика". Москва, "Пранд",
   1999
   2. Ю.А.Ершов, В.А.Попков, А.С.Берлянд, А.З.Книжник,
   Н.И.Михайличенко, "Биофизическая химия". Москва, "Высшая
   школа", 1993
   3. А.Н.Герасимов, "Математические модели в биологии, экологии и
   медицине. Москва, МИФИ, 1998
   4. А.О.Рувинский, Л.В.Высоцкая, С.М.Глаголев и др., "Общая биоло-
   гия". Москва, "Просвещение", 1993

Со всеми вопросами и предложениями просьба обращаться:
e-mail: rualark@gmail.com

                                               Архипенко Алексей
                                               Москва
                                               1999

Project Members:

• Alexey (admin)